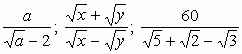Négyzetre emeléskor egy számot önmagával szorzunk meg, ezért az eredmény soha sem lehet negatív: 02=0, 52=25, (−5)2=25, minden a valós számra teljesül az |a|
ł 0 összefüggés. A négyzetgyökvonás a négyzetre emelés fordított (inverz) művelete, ezért csak a nem negatív számok körében végezhető el. Egy nem negatív a valós szám négyzetgyökén azt a nem negatív valós számot értjük, amelynek a négyzete a. Példák:![]() , mert 3ł 0 és 32=9,
, mert 3ł 0 és 32=9,
![]() , mert 0ł 0 és 02=0,
, mert 0ł 0 és 02=0,
![]() , mert 1,3ł 0 és 1,32=1,69,
, mert 1,3ł 0 és 1,32=1,69,
![]() nincs értelmezve, mert −16<0, nem létezik olyan valós szám, amelynek a négyzete negatív,
nincs értelmezve, mert −16<0, nem létezik olyan valós szám, amelynek a négyzete negatív,
![]() , mert x2ł 0 és (x2)2=x4,
, mert x2ł 0 és (x2)2=x4,
![]() , mert |a|ł 0 és |a|2=a2.
, mert |a|ł 0 és |a|2=a2.
Felhívjuk a figyelmet egy gyakori félreértésre: az x2=4 egyenlet megoldása nem csak a 4 négyzetgyöke (a 2), hanem a 2 és a −2. Ugyanis azok a számok elégítik ki az x2=4 egyenletet, amelyeknek a négyzete 4. Másképpen: az x2=4 egyenlet az |x|=2 egyenlettel ekvivalens, ezért gyökei a 2 és a −2.
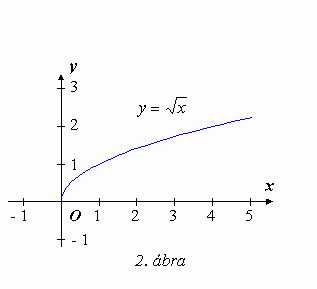
Korábbról ismerjük a négyzetre emelés és a négyzetgyökvonás függvényét. Az 1. és 2. ábrán ezek grafikonja látható.
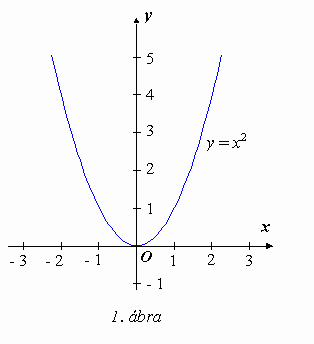
A négyzetgyökvonás azonosságai
Megkönnyíti a négyzetgyökökkel való számolást, ha megjegyzünk néhány műveleti azonosságot:
I. ![]() , a
, a
II. ![]() , a
, a
III. ![]() , a
, a
Példa a második azonosság alkalmazására: ![]() .
.
Műveletek négyzetgyökös kifejezésekkel
Oldjunk meg néhány feladatot a négyzetgyökvonás azonosságainak segítségével!
Példák:
A tanult azonosságok alkalmazásával elvégezzük az alábbi műveleteket:
a) ![]()
b) ![]()
c) 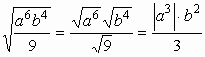
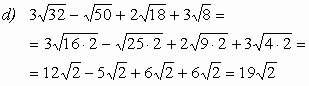

Feladatok
Végezzük el a következő műveleteket!
1. ![]() ,
, ![]()
![]()
2. 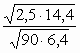 ,
, ![]() ,
, ![]()
3. ![]() ,
, 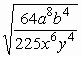
Az alábbi feladatokban emeljük ki a négyzetgyök elé, amit lehet!
4. ![]()
5. ![]()
6. ![]()
A négyzetgyökjel alá vitellel hozzuk egyszerűbb alakra a következő kifejezéseket!
7. ![]()
8. 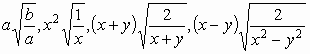
Végezzük el a következő műveleteket!
9. ![]()
10. ![]()
11. ![]()
12. 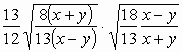
13. ![]()
14. ![]()
15. 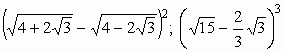
16. ![]()
17. ![]()
Speciális négyzetgyökökkel végzett művelet a tört számlálójának, vagy nevezőjének gyöktelenítése. Az alábbi néhány példában úgy alakítjuk át a törteket, hogy átalakítás után a nevezőben ne legyen gyökvonás kijelölve:
![]() , a nevezővel bővítve értük el a kívánt eredményt.
, a nevezővel bővítve értük el a kívánt eredményt.
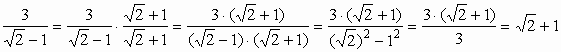 , az (a+b)(a−b)=a2−b2 azonosságot alkalmazva bővítettük a törtet. Ha egy kéttagú összeg egyik tagjának megváltoztatjuk az előjelét, akkor a az így kapott kifejezést az eredeti kifejezés konjugáltjának nevezzük. Kéttagú nevező esetén mindig célra vezet a nevező konjugáltjával való bővítés.
, az (a+b)(a−b)=a2−b2 azonosságot alkalmazva bővítettük a törtet. Ha egy kéttagú összeg egyik tagjának megváltoztatjuk az előjelét, akkor a az így kapott kifejezést az eredeti kifejezés konjugáltjának nevezzük. Kéttagú nevező esetén mindig célra vezet a nevező konjugáltjával való bővítés.
Egy nehezebb példa:
Gyöktelenítsük a ![]() törtet!
törtet!
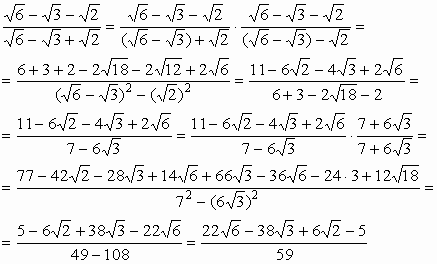
Kétszeri bővítés (és sok számolás) után kaptuk meg a végeredményt.
Feladatok
Gyöktelenítsük az alábbi törtek nevezőjét!
18. ![]()
19. 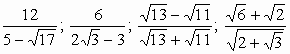
20.