Már korábban is oldottunk meg egyenleteket. Ezek többsége elsőfokú, vagy ekvivalens lépésekkel elsőfokúvá alakítható volt. Ismétlésként oldjunk meg néhány feladatot!
Feladatok
Oldjuk meg az alábbi egyenleteket!
45.
46. 
47. 
48. 
49. 
50. 
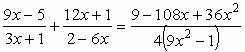
Néhány magasabbfokú egyenlettel is találkoztunk, ezeket a szorzattá alakítás módszerével oldottuk meg.
Példa:
Oldjuk meg az x2+5x+6=0 egyenletet!
A megoldás lényege, hogy a bal oldali kifejezést szorzattá alakítjuk csoportosítással és kiemeléssel:
x2+5x+6=x2+2x+3x+6=x(x+2)+3(x+2)=(x+2)(x+3). Egy szorzat értéke akkor és csak akkor 0, ha valamelyik tényezője 0. Ezért az x+2 vagy x+3 kifejezés értéke 0, azaz az egyenlet gyökei x1=−2; x2=−3.
Egyszerűbb esetekben ez a módszer célravezető, bár helyenként nagy fantáziát igényel. Egy olyan módszert ismertetünk a hasonló egyenletek megoldására, ami minden esetben használható: az eljárásban az (a
± b)2=a2± 2ab+b2 azonosság segítségével teljes négyzetté egészítjük a másodfokú kifejezést, majd az a2-b2=(a+b)(a−b) azonosság alkalmazásával végezzük el a tényezőkre bontást. Példaként megoldjuk az x2−4x+3=0 egyenletet:x2−4x+3=(x−2)2−22+3, az első két tag néggyel (a kettő négyzetével) kevesebb (x−2)2-nél, ezért x2−4x=(x−2)2−22.
(x−2)2−22+3=(x−2)2−12=(x−2+1)(x−2−1)=(x−1)(x−3). Az (x−2)2−12 kifejezésre alkalmaztuk a két négyzetszám különbségének szorzattá alakítására vonatkozó azonosságot. Innen az x1=1; x2=3 gyököket kapjuk.
Oldjuk meg így is az x2+5x+6=0 egyenletet!
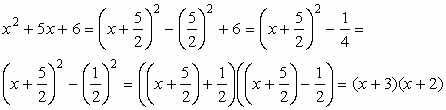
Innen természetesen újra az x1=−2; x2=−3 megoldások adódnak.
Lássunk még egy feladatot:
Oldjuk meg az x2+2x+3=0 egyenletet a valós számok halmazán!
x2+2x+3=(x+1)2−1+3=(x+1)2+2. Ennek az egyenletnek nincs megoldása, mert egy négyzetes kifejezés mindig nem negatív, ehhez kettőt adva sohasem kaphatunk nullát.
A fenti módszer a másodfokú egyenletek megoldása teljes négyzetté egészítéssel néven ismeretes.
Feladatok
Oldjuk meg az alábbi másodfokú egyenleteket teljes négyzetté egészítéssel!
51. 
52. 
53. 
54. 
55. 
56. 
57. 
58. 
A másodfokú egyenlet megoldóképlete
A teljes négyzetté egészítés minden másodfokú egyenletre alkalmazható, általános módszer. Ha az egyenletben az együtthatókat betűkkel jelöljük (paraméteres egyenlet), és így végezzük el a megoldást, akkor végül egy képlethez jutunk, amelyből egyszerű behelyettesítéssel számolhatók a gyökök. A másodfokú egyenlet kanonikus alakja: 
, ahol az a, b, c együtthatók valós számok és a értéke nem lehet 0 (ellenkező esetben az egyenlet nem lenne másodfokú). Ezt az egyenletet fogjuk megoldani. A levezetés közben az egyes lépések elvégzésekor tekintettel kell lennünk az együtthatók összes lehetséges értékeire.
Első lépésként a bal oldalon a-t kiemelünk:
, ezután a zárójelben az első két tagot teljes négyzetté alakítjuk:
.
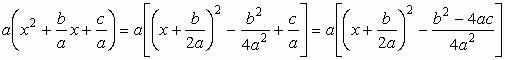A megoldás további menete a 
kifejezés előjelétől függ:
ha <0, akkor a szögletes zárójelben biztosan pozitív szám áll, ezért az egyenletnek nincs megoldása,
ha =0, akkor a kerek zárójelben levő kifejezésnek kell nullával egyenlőnek lennie, ezért egy megoldás van, az 
,
ha >0, akkor a 
tört felírható 
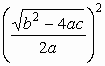alakban. A megoldás további menete:
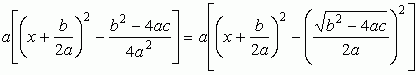
szorzattá bontjuk a szögletes zárójelben levő részt:
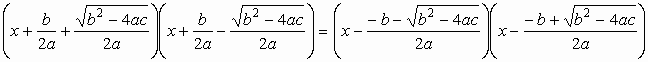Így az eredeti egyenlet a következő alakot ölti:
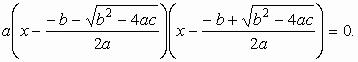
Mivel a nem lehet nulla, a két zárójeles kifejezés értéke lesz nulla, azaz az egyenlet gyökei:
A két gyököt egyetlen formulával is megadhatjuk, így kapjuk a másodfokú egyenlet megoldóképletét: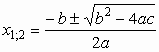 
.
A megoldásban fontos szerepet játszott az egyenlet együtthatóiból képzett 
kifejezés. Ennek neve diszkrimináns (meghatározó, döntő tényező), jele: D. A diszkrimináns előjele határozza meg az egyenlet gyökeinek számát:
Néhány példa a megoldóképlet alkalmazására:
Oldjuk meg az alábbi másodfokú egyenleteket a megoldóképlet segítségével!
a) x2−5x+6=0
Először meghatározzuk az együtthatók konkrét értékét: a=1, b= −5, c=6, majd kiszámítjuk a diszkriminánst (előbb-utóbb mindenképpen ki kell számítanunk, de negatív diszkrimináns esetén némi munkát megspórolhatunk): D=b2−4ac=(−5)2−4
× 1× 6=1. Ezután alkalmazzuk a megoldóképletet:
, innen a gyökök: x1=3, x2=2.
b) x2−6x+9=0
a=1, b=−6, c=9
Ţ D= (−6)2−4× 1× 9=0 Ţ
, azaz az egyenletnek két egybeeső valós gyöke van.
c) −2x2+5x+6=0
a=−2, b=5, c=6
Ţ D=52−4× (−2) 6=−23 Ţ az egyenletnek nincs valós gyöke, mert a diszkrimináns negatív.Feladatok
Oldjuk meg az alábbi egyenleteket a megoldóképlet segítségével!
59. 
60. 
61. 
62. 
63. 
64. 
Gyakori eset, hogy a megoldóképlet alkalmazása előtt az egyenletet kanonikus alakra kell hoznunk.
Példa:
Először szorzattá alakítjuk a nevezőket :
.
Majd meghatározzuk az egyenlet alaphalmazát: a nevezőben nem állhat nulla, ezért xą −1 és xą 1. Ezután szorzunk a nevezők legkisebb közös többszörösével, ebben az esetben (x+1)(x−1)-gyel:
6+(x+1)=3(x+1)(x−1), rendezzük az egyenletet:
7+x=3x2−3
0=3x2−x−10, kiszámítjuk a diszkriminánst: D=1−4× 3× (−10)=121, végül a megoldóképlet következik: 
. Innen a gyökök: x1=2, 
. Mivel ekvivalens átalakításokat végeztünk és mindkét gyök eleme az alaphalmaznak, ezért az eredeti egyenletnek két különböző megoldása van. Most elvileg ugyan nem szükséges ellenőrizni a kapott gyököket, de gyakorlati szempontból ajánlatos.
Feladatok
65. 
66. 
67. 
68. 
69. 
A másodfokú egyenlet gyöktényezős alakja
A megoldóképlet levezetése közben − a Dł 0 esetben − eljutottunk a következő sorhoz:
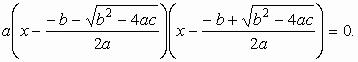
A gyökök szokásos jelölésével írhatjuk a következőt:
, ha Dł 0. A D=0 esetben x1=x2. Innen is látható, hogy egy valós gyök esetén célszerű ezt a gyököt kettős gyöknek tekinteni ( két egyenlő gyök). Az a(x−x1)(x−x2) alakot a másodfokú egyenlet gyöktényezős alakjának nevezzük. A gyöktényezős alak segítségével könnyen és gyorsan szorzattá bonthatjuk a másodfokú kifejezéseket.
Példák:
Bontsuk fel elsőfokú tényezőkre az alábbi polinomokat!
a) 2x2+5x−3
Elsőként meghatározzuk a polinom zérushelyeit, azaz megoldjuk a 2x2+5x−3=0 másodfokú egyenletet: D=52−4× 2× (−3)=49, alkalmazva a megoldóképletet az x1=−3 és az 
gyökökhöz jutunk. A gyöktényezős alak: 
. Ezt az eredményt egyszerűbb (szebb) alakban is felírhatjuk, ha a 2-vel megszorozzuk a második zárójeles tényezőt: (x+3)(2x−1).
b) x2+4x+4
A zérushelyek meghatározásakor az x1=x2=−2 eredmény adódik, ezért a szorzat alak: (x+2)(x+2)=(x+2)2.
c) x2+2x+4
D=−12. Mivel a diszkrimináns negatív, a polinom nem bontható fel elsőfokú tényezők szorzatára!
Feladatok
70. Írjunk fel olyan másodfokú egyenleteket, amelyeknek a következő számpárok a gyökei: (5; 8), (−4; −5), 
!
71. Bontsuk fel elsőfokú tényezők szorzatára az alábbi polinomokat: 
, 
, 
!
72. Egyszerűsítsük a következő törteket: 
, 
, 
!
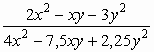A másodfokú egyenlőtlenségek megoldására két módszert ismertetünk: egy “lényegében” grafikus és egy “lényegében” algebrai eljárást. Példaként mindkét módszerrel megoldjuk az x2−2x−3<0 egyenlőtlenséget.
I. Grafikus megoldás
Vázlatosan ábrázoljuk az 
függvényt, majd a grafikonról olvassuk le a megoldást. Tudjuk, hogy a másodfokú függvény képe parabola. Most csak a parabola állását kell ismernünk (felfelé vagy lefelé nyitott), valamint a zérushelyeket. A parabola állását a négyzetes tag együtthatójának előjele határozza meg, ez most pozitív, ezért egy felfelé nyitott parabolával van dolgunk. A zérushelyek meghatározásához az x2−2x−3=0 egyenletet kell megoldanunk: x1=−1, x2=3 adódik. A 7. ábráról leolvashatjuk a megoldást.
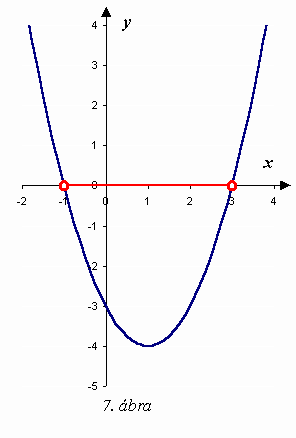
A megoldás a ]−1; 3[ nyílt intervallum (−1<x<3).
II. Algebrai megoldás
Ezt a megoldást is a zérushelyek kiszámításával kezdjük: x1=−1, x2=3. Ezután a másodfokú egyenlet gyöktényezős alakja segítségével szorzattá alakítjuk az egyenlőtlenség bal oldalát: (x+1)(x−3)<0. Egy szorzat akkor és csak akkor negatív, ha tényezői között páratlan sok negatív szerepel, esetünkben egy. A lehetséges esetek áttekintését megkönnyíti, ha az egyes tényezők előjelét számegyenesen ábrázoljuk (8. ábra):
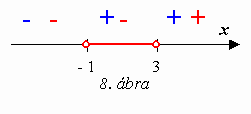
Kék színnel jelöltük az első, pirossal a második tényező előjelét. A számegyenesről közvetlenül leolvashatjuk a megoldást: −1<0<3.
Mindkét módszer alkalmas összetettebb egyenlőtlenségek megoldására is. Lássunk egy bonyolultabb példát: oldjuk meg a pozitív számok halmazán a 
egyenlőtlenséget! Nullára redukáljuk az egyenlőtlenséget, majd közös nevezőre hozunk:
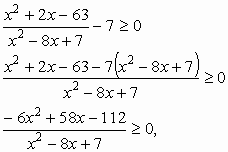
mindkét oldalt elosztjuk −2-vel (nem feledkezünk el a relációjel megfordításáról!):
Meghatározzuk a számláló és a nevező zérushelyeit: x1=7 és 
a számláló, x3=7 és x4=1 a nevező zérushelyei. Mivel a nevező nem lehet nulla ezért az egyenlőtlenség alaphalmaza R+\{1; 7}. Ettől a ponttól kezdve nézzük a kétféle befejezést.
I. Grafikus módszer
Ábrázoljuk közös koordinátarendszerben az 
és az 
függvényeket (9. ábra)!
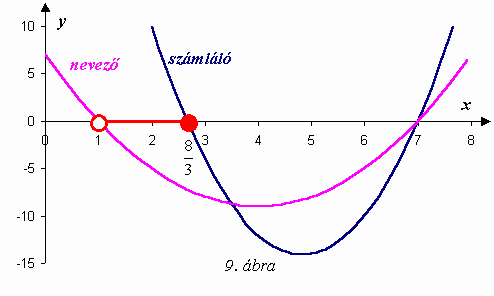
Egy tört értéke akkor lehet 0, ha a számlálója 0, akkor lehet negatív ha számlálója és nevezője különböző előjelű. Figyelembe véve az alaphalmazt is, a megoldás a grafikonról leolvasható: 
.
II. Algebrai módszer
A gyöktényezős alak segítségével szorzattá alakítjuk a számlálót és a nevezőt:
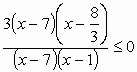, (x−7)-tel egyszerűsítünk és 3-mal osztunk: 
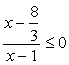. A számláló és a nevező előjelét számegyenesen ábrázoljuk (10. ábra), majd a rajzról leolvassuk a megoldást: . (Kék színnel jelöltük a számláló, piros színnel a nevező előjelét.)
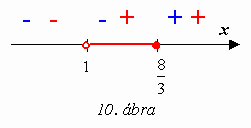
Ebben az esetben a második módszer elegánsabbnak bizonyult.
Feladatok
Oldjuk meg a valós számok halmazán az alábbi egyenlőtlenségeket!
73. 
74. 
75. 
76. 
77. 
78. 
79. 
80. 
81. 
82. 
Összefüggések a másodfokú egyenlet gyökei és együtthatói között
(Vičte
Hasonlítsuk össze a másodfokú egyenlet gyöktényezős és kanonikus alakját: 
. Bontsuk fel a gyöktényezős alakban szereplő zárójeleket és rendezzük a szokásos módon − az x hatványai szerint − a kapott polinomot:
. Az így kapott alakot egybevetve a kanonikus alakkal, két összefüggést írhatunk fel az együtthatók egyenlősége alapján:
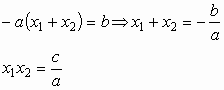
Ezeket a gyökök és együtthatók közötti összefüggéseket
François Vičte francia matematikus tiszteletére Vičte-formuláknak nevezzük.A formulák természetesen csak abban az esetben érvényesek, ha az egyenletnek van valós gyöke, azaz D
ł 0.Példák:
a) Határozzuk meg a 2x2−3x−3=0 egyenlet gyökeinek négyzetösszegét!
Először megvizsgáljuk az egyenlet diszkriminánsát: D=33>0, azaz az egyenletnek két különböző valós gyöke van. A feladatot kétféleképpen oldjuk meg.
I megoldás:
A megoldóképlettel kiszámítjuk a gyököket, majd ezután meghatározzuk a négyzetösszeget: 
.
II. megoldás:
A Vičte-formulák segítségével kifejezzük a gyökök négyzetösszegét: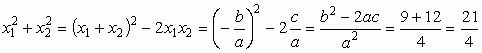 
.
A két megoldás ebben az esetben körülbelül ugyanannyi munkát vett igénybe.
b) Mekkorának válasszuk c-t, hogy az x2+(3c+1)x+4c=0 egyenlet gyökeinek négyzetösszege 
legyen?
Először meghatározzuk a megoldhatóság feltételét (Dł 0): 
ł 0. Gondolkodjunk el a megoldás további menetén! Két lehetőség közül választhatunk:
feltétel vizsgálatára, végül ellenőrizzük, hogy az utóbbi feltételből kapott c érték eleget tesz-e az egyenlőtlenségnek. 
feltételt vizsgáljuk meg, majd ezután egyszerű behelyettesítéssel ellenőrizzük, hogy a kapott c érték kielégíti-e az egyenlőtlenséget.
Elvi különbség ugyan nincsen a két változat között, de a második módszer valószínűleg kevesebb munkát igényel, ezért ezt választjuk. Most is kétféleképpen fejezzük be a feladatot.
I. megoldás
Alkalmazzuk a megoldóképletet: 
. Kifejezzük a gyökök négyzetösszegét:
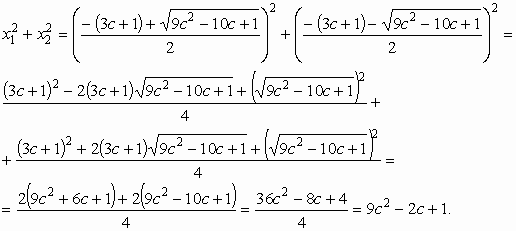
Ezután megoldjuk a 
másodfokú egyenletet. Hárommal való szorzás és nullára redukálás után: 
. A megoldóképletből a 
értékek adódnak. 
esetén az eredeti egyenlet diszkriminánsa negatív, ezért ez nem megoldása a feladatnak, 
esetén pozitív a diszkrimináns, tehát a feladat egyetlen megoldása: 
.
Ebben a megoldásban elég sokat kellet számolni, nézzük a másik lehetőséget:
II. megoldás
A gyökök és együtthatók közötti összefüggéseket alkalmazzuk:
.
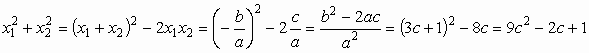Innen ugyanúgy fejezzük be a megoldást, mint az előző esetben.
A kétféle megoldás összevetéséből kitűnik, hogy ebben az esetben a Vičte-formulák használata lényegesen lerövidítette a számolást.
Feladatok
83. Határozzuk meg p-t úgy, hogy az 
egyenlet két gyökének összege 10 legyen!
84. A 
egyenlet egyik gyöke a másik ellentettje. Melyek ezek a gyökök?
85. Mennyi a 
egyenlet gyökei reciprokának az összege?
86. Mennyi az 
egyenlet valós gyökeinek a négyzetösszege?
87. A t valós paraméter mely értékeire lesz a 
egyenlet gyökeinek a négyzetösszege 1,25?
88. A 
egyenlet megoldása nélkül számítsuk ki az 
kifejezés értékét, ahol x1 és x2 az egyenlet két gyöke!
89. A p valós paraméter mely értékénél lesz az 
egyenletben a gyökök négyzetösszege minimális?
Az olyan egyenleteket, amelyekben az együtthatók némelyike ismertnek tekinthető betű, paraméteres egyenleteknek nevezzük. Ilyen egyenlet a másodfokú egyenlet kanonikus alakja is: 
. A megoldóképlet levezetésekor láthattuk, hogy különösen gondosan kell eljárni az ilyen egyenletek megoldásakor. A paraméteres másodfokú egyenletekkel kapcsolatos feladatokban előfordul, hogy nem kell megoldanunk az egyenletet, hanem egyéb kérdésekre kell választ adnunk. Tipikus feladat, amikor az egyenlet megoldásainak számát vizsgáljuk a paraméterek függvényében, vagy az egyenlet gyökeiből képzett kifejezéseknek kell előírt értéket felvenniük (lásd az előző alfejezet b) példáját!).
Feladatok
90. Határozzuk meg c-t úgy, hogy a 
egyenletnek
a) két egyenlő gyöke legyen,
b) két pozitív gyöke legyen,
c) egy pozitív és egy negatív gyöke legyen,
d) egyik gyöke 0 legyen,
e) ne legyen valós gyöke!
91. Milyen valós k értéknél lesz az
a) 
egyenlet egyik gyöke −2,
b) 
egyenlet egyik gyöke 5,
c) 
egyenlet egyik gyöke 3,
d) 
egyenlet egyik gyöke −0,1,
e) 
egyenlet egyik gyöke a+b?
92. A p valós paraméter mely értékeire lesz a 
egyenletnek
a) két különböző gyöke,
b) két egyenlő abszolút értékű gyöke,
c) két egyenlő gyöke?
93. Határozzuk meg k értékét a 
egyenletben úgy, hogy az egyenlet egyik gyöke a másik gyök kétszerese legyen!
94. Oldjuk meg az 
egyenletet! Van-e olyan p érték, amelyre az egyenletnek nincs valós gyöke?
Másodfokúra visszavezethető egyenletek
Gyakran előfordul, hogy egy-egy 2-nél magasabb fokszámú egyenletet másodfokúra vezethetünk vissza egy új ismeretlen bevezetésével. Néhány példán keresztül áttekintjük a gyakoribb eseteket.
Az 
alakúra hozható egyenleteket könnyen megoldhatjuk, ha x2 helyett egy új ismeretlent vezetünk be. Példa:
Oldjuk meg az x4−5x2+4=0 egyenletet a valós számok halmazán!
Az y=x2 ismeretlen bevezetésével egyenletünk y2−5y+4=0 alakú lesz. Alkalmazva a megoldóképletet y-ra az 1 és 4 gyököket kapjuk. Innen az eredeti egyenlet megoldásai: −1; 1; −2; 2.
Vannak olyan egyenletek, amelyeknek valamely valós számmal együtt az illető szám reciproka is megoldása, ezeket az egyenleteket nevezzük reciprokegyenletnek. Tekintsünk egy általános negyedfokú egyenletet:
. Ha ez reciprokegyenlet, akkor a 0 nem lehet gyöke (ugyanis a nulla reciproka nem értelmezhető), tehát eą 0. x helyére helyettesítsük a reciprokát, majd szorozzuk meg az egyenletet x4-nel: 
.
Az eredeti és az új egyenlet gyökei megegyeznek, ezért a két egyenlet megfelelő együtthatóinak is meg kell egyezniük, azaz a=e, b=d. Eszerint a negyedfokú reciprokegyenlet általános alakja:
, ahol aą 0. Ügyes helyettesítéssel ez az egyenlet másodfokúra vezethető vissza. Osszuk el az egyenletet x2-tel, majd rendezzük át a tagokat:
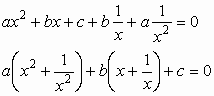
Ha bevezetjük az 
új ismeretlent, akkor az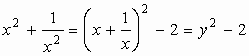 
összefüggés alapján az 
másodfokú egyenlethez jutunk. Ezt megoldjuk y-ra, majd két újabb másodfokú egyenlet megoldásával kapjuk az eredeti egyenlet gyökeit.
Példa:
Oldjuk meg a 6x4−13x3+12x2−13x+6=0 egyenletet a valós számok halmazán!
Észrevesszük, hogy reciprokegyenletről van szó, ezért osztunk x2-tel, majd átrendezzük a tagokat:
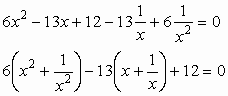
Ha 
, akkor 
, így a 6(y2−2)−13y+12=0 egyenlet adódik. Ezt rendezzük: 6y2−13y=0, ezután szorzattá alakítunk: y(6y−13)=0. Innen az y1=0, 
gyökök adónak. A 0 nyilvánvalóan hamis gyök (semmilyen számnak és a reciprokának összege nem lehet 0), ezért csak az 
egyenletet kell megoldanunk. 6x-szel való szorzás és rendezés után: 6x2−13x+6=0. Ennek, és egyszersmind az eredeti egyenletnek a megoldásai: 
.
Gyakran egy-egy feladat megoldásához egyszeri ötlet szükséges. Egyetlen példát nézünk meg:
Oldjuk meg a 
egyenletet!
Először az alaphalmazt határozzuk meg: x2−4x+10
ą 0. D=−24<0, ezért a nevező sosem lesz 0, az egyenlet alaphalmaza R. alaposabban szemügyre véve az egyenletet, észrevehetjük, hogy célszerű az y=x2−4x+6 helyettesítést elvégezni. Ezután egyenletünk a következő alakú lesz:
. Szorzunk a nevezővel és rendezünk: −y2−4y+21=0. A megoldóképlet alkalmazása előtt célszerű −1-gyel szorozni: y2+4y−21=0. Innen a gyökök: y1=3, y2=−7. Befejezésül a 3= x2−4x+6, illetve a −7= x2−4x+6 egyenleteket kell megoldanunk. Az első egyenletből x1=1, x2=3 adódik, a második egyenletnek negatív a diszkriminánsa, ezért abból nem kapunk gyököt. Az eredeti egyenlet gyökei. x1=1, x2=3.
A Mezopotámiából származó kb. 4000 éves ékírásos szövegekből kiderül, hogy már akkor oldottak meg másodfokú egyenleteket.
A XV−XVI. századi olasz matematikusok értek el maradandó eredményeket a harmad- illetve negyedfokú egyenletek megoldásában. A bolognai matematikusok a harmadfokú egyenleteket három típusra osztották, illetve vezették vissza. Ezek vizsgálatával foglalkozott többek között a bolognai egyetem professzora, Scipione del Ferro (1465?−1526) is, aki valószínűleg mindhárom típust megoldotta, de eljárása nem maradt fenn. Halála után
Tartaglia újból felfedezte a harmadfokú egyenlet megoldását. Eljárását közölte Cardanoval, aki 1545-ben megjelent Ars Magna című művében ismertette a módszert. (Az algoritmus azóta Cardano-képlet néven ismeretes.) Az általános negyedfokú egyenlet harmadfokúra való visszavezetése Ludovico Ferrari érdeme.A XIX. században elsősorban
Abel norvég, és Galois francia matematikusok kutatásai tisztázták az algebrai egyenletek megoldhatóságának feltételeit. E kutatások egyik érdekes eredménye, hogy az általános ötöd- vagy magasabbfokú egyenletek nem oldhatók meg az alapműveletek és a gyökvonás véges sokszori alkalmazásával, az ilyen egyenletekre nem létezik megoldóképlet.Feladatok
Oldjuk meg az alábbi egyenleteket!
95. 
96. 
97. 
98. 
99. 
100. 
101. 
Másod- és magasabbfokú egyenletrendszerek
A másod- és magasabbfokú egyenletrendszerek megoldása nem igényel új elméleti ismereteket, de helyenként éles szemre van szükség. Lássunk egy példát:
Oldjuk meg az alábbi egyenletrendszert a valós számpárok halmazán!
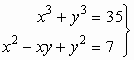
Az egyenlő együtthatók módszerét nyílván nem alkalmazhatjuk. Ha valamelyik egyenletből kifejezzük az egyik ismeretlent, akkor bonyolult, nehezen kezelhető kifejezést kapunk. Próbálkozzunk valami mással! Némi töprengés után észrevehetjük, hogy az első egyenlet bal oldala szorzattá alakítható, és az egyik tényező éppen a második egyenlet bal oldala lesz: 
. Felhasználva ezt az összefüggést osszuk el az első egyenletet a másodikkal!
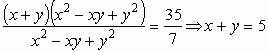, ebből az egyenletből már könnyen kifejezhetjük az egyik ismeretlent: y=5−x. Helyettesítsünk be a második egyenletbe:
, rendezzük az egyenletet: 
. A megoldóképlet a 2 és 3 gyököket szolgáltatja. Kiszámítva a megfelelő y-okat az egyenletrendszernek két pár megoldása van: (2; 3) és (3; 2).
Feladatok
Határozzuk meg a következő egyenletrendszerek megoldásait a valós számpárok halmazán!
102. 
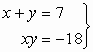
103. 
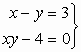
104. 
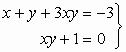
105. 
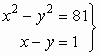
106. 
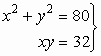
107. 
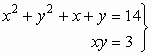
108. 
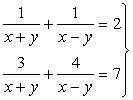
109. 
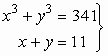
Sok szöveges feladat másodfokú egyenletre vagy egyenletrendszerre vezet.
Példák:
a) Egy kétjegyű szám számjegyeinek az összege 9. Ha a számjegyeket felcseréljük, és az így kapott számot az eredetivel megszorozzuk, eredményül 2268-at kapunk. Melyik ez a két szám?
Foglaljuk táblázatba a tudnivalókat!
|
|
1. számjegy |
2. számjegy |
|
eredeti szám |
x |
9−x |
|
“új” szám |
9−x |
x |
Az eredeti szám értéke: 10x+(9−x)=9x+9=9(x+1), a számjegyek felcserélésével kapott szám értéke: 10(9−x)+x=90−9x=9(10−x). Most már könnyen felírhatjuk az egyenletet: 9(x+1)
× 9(10−x)=2268. 81-gyel osztva és rendezve: x2−9x+18=0, ennek gyökei a 3 és a 6. A kétjegyű számok 36 illetve 63. Szöveges feladat megoldásakor ne feledkezzünk el a kapott eredményeket az eredeti szöveg alapján ellenőrizni! Most nagyon egyszerű az ellenőrzés: 63× 36=2268.b) Egy 12 cm×18 cm méretű fénykép körül egyenlő szélességű keret van. Határozzuk meg a keret szélességét, ha területe egyenlő a kép területének 75%-ával!
Egy ábrán tűntessük fel a megadott paramétereket, a keret szélességét jelöljük x-szel:
Mivel a keret területe 75%-a a kép területének, a keret és a kép együttes területe 175%-a a kép területének. A kép területe 12 cm × 18 cm = 216 cm2, a keret és a kép együttes területe (2x+12 cm)×(2x+18 cm), így az egyenlet: (2x+12)(2x+18)=1,75
× 216. Elvégezve a kijelölt műveleteket és rendezve az egyenletet: 2x2+30x−81=0. Az egyik gyök negatív, ez nyílván nem lehet megoldása az eredeti feladatnak, a másik gyök közelítő értéke 2,3. Tehát a keret szélessége kb. 2,3 cm.Feladatok
110. Két egymást követő természetes szám szorzata 552. Melyik ez a két szám?
111. Egy tört számlálója 2-vel kisebb, mint a nevezője. Ha ehhez a törthöz hozzáadjuk a reciprokát, akkor 
-öt kapunk. Melyik ez a tört?
112. Határozzuk meg azt a kétjegyű számot, amelyben az egyesek száma 2-vel nagyobb a tízesek számánál, és ha a számot megszorozzuk a számjegyeinek összegével, akkor 144-et kapunk!
113. Egy árú árát felemelték, majd később kétszer annyi százalékkal csökkentették, mint ahány százalékkal felemelték annak idején. Hány százalékkal emelték az árát eredetileg, ha végül 5,5 %-kal lett olcsóbb?
114. Egy tartály két csövön keresztül 6 óra alatt telik meg. Az egyik csövön át 5 órával hamarabb telne meg, mint a másikon. Mennyi idő alatt töltené meg a két cső külön-külön a tartályt?
115. Két kikötő között a távolság egy folyón 21 km. Egy motorcsónak elindul az egyik kikötőből a másikba, ott 30 percet áll, majd visszaindul, és így az első indulás után 4 órával ér vissza. Mekkora a motorcsónak sebessége állóvízben, ha a folyó 2,5 km/h sebességgel folyik?
A négyzetgyökös kifejezést tartalmazó egyenletek sokszor visszavezethetők másodfokúra egy-két négyzetre emelés után. Gyökös egyenletek alaphalmazának vizsgálatakor körültekintően kell eljárnunk: tudjuk, hogy csak a nem negatív számok négyzetgyöke értelmezhető. Megoldás közben általában nem kerülhető el a négyzetre emelés, de ezzel a lépéssel is óvatosan kell bánnunk. A négyzetre emelés csak akkor ekvivalens átalakítás, ha az egyenlet mindkét oldalán azonos előjelű kifejezések állnak. Minden egyéb esetben elvileg is szükséges ellenőrizni a megoldásokat.
Példa:
Oldjuk meg a valós számok halmazán a 
egyenletet!
Egyik négyzetgyök alatti kifejezés sem lehet negatív, ezért xł 0, x−5ł 0 és 10−xł 0. Innen xł 0, xł 5 és 10ł x. Mindhárom feltételnek teljesülnie kell, tehát 10ł xł 5. Négyzetgyökös kifejezés értéke sem lehet negatív, ezért az egyenlet mindkét oldala nem negatív, azaz most a négyzetre emelés ekvivalens lépés:
,
ezután úgy rendezzük az egyenletet, hogy az egyik oldalon csak a négyzetgyököt tartalmazó kifejezés maradjon:
.
Mivel a bal oldali kifejezés nem negatív, a jobb oldal sem lehet negatív: 15−3xł 0. Ebből 5ł x. Egybevetve a megoldás elején tett kikötéssel, az adódik, hogy az x egyetlen elvileg lehetséges értéke 5. Elegendő az x=5 értéket behelyettesítéssel ellenőrizni. Az ellenőrzés azt mutatja, hogy az 5 kielégíti az egyenletet, ezért az egyetlen megoldás: x=5.
Tanulságos a egyenletet más úton is megoldani. A jobb oldal előjelének vizsgálata nélkül emeljünk négyzetre, de tartsuk észben, hogy a végén majd ellenőriznünk kell a lehetséges megoldásokat, hiszen a négyzetre emelés most nem ekvivalens átalakítás.
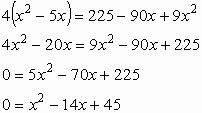
Megoldva az egyenletet: x1=5, x2=9. Mindkét gyök eleget tesz az előzetes kikötéseknek, csak az eredeti egyenletbe való visszahelyettesítéskor derül ki, hogy a 9 nem megoldás. Így az egyetlen helyes megoldás az x=5.
Feladatok
Oldjuk meg a valós számok halmazán az alábbi egyenleteket!
116. 
117. 
118. 
119. 
120. 
121. 
122. 