, mert 33=27,Ahogy a négyzetgyökvonás a négyzetre emelés inverz művelete, értelmezhetjük a köbre emelés, negyedik hatványra emelés stb. inverz műveleteit is. Mivel pozitív, páros egész hatványkitevő esetén a hatvány előjele nem lehet negatív, páratlan kitevő esetén azonban igen, külön kell definiálnunk a páros és páratlan kitevőjű gyököket:
Egy nem negatív a valós szám 2k-adik (k pozitív egész szám) gyökén azt a nem negatív számot értjük, amelynek 2k-adik hatványa a.
Egy a valós szám (2k+1)-edik (k pozitív egész szám) gyökén azt a számot értjük, amelynek (2k+1)-edik hatványa a.
Néhány példa:
, mert 33=27,
,
,
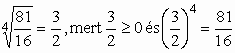nincs értelmezve, mert −1<0.
Feladatok
Végezzük el az alábbi gyökvonásokat!
21. 
22. 
23. A változó milyen értékeire teljesülnek a következő egyenlőségek?
A
négyzetgyökvonás azonosságaival analóg összefüggések teljesülnek az n-edik gyökökkel való számolásra is: I. 
II. 
III. 
A fenti azonosságok könnyen igazolhatók a definíciók alapján.
Most megvizs
gáljuk, hogy hogyan vonhatunk gyököt gyökös kifejezésből. Egy konkrét példa alapján megfogalmazzuk az állítást, majd a sejtést bebizonyítjuk. Három gyökös kifejezés értékét határozzuk meg: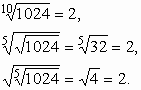 
Állítás: 
Bizonyí
tás: Elsőként megállapíthatjuk, hogy mindhárom kifejezés értelmezési tartománya egyenlő. Ha n és m közül legalább az egyik páros, akkor a nem negatív szám, egyébként tetszőleges valós szám. Így elegendő belátni, hogy az egyes kifejezések nm-edik hatványai egyenlők. Az átalakítás során felhasználjuk az n-edik gyök definícióját és a hatványozás azonosságait: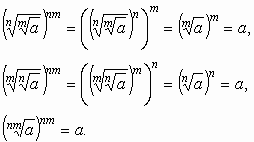
Az alábbi feladatcsoportok megoldását egy-két példa segíti.
Feladatok
A gyökjel alól való kiemeléssel hozzuk egyszerűbb alakra a következő kifejezéseket! (Az egyszerűség kedvéért a változók nem negatívok.)
Példák:
a) 
b) 
24. 
25. 
26. 
A gyökjel előtt álló kifejezéseket vigyük a gyökjel alá!
Példa: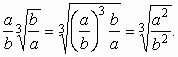 
27. 
28. 
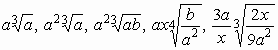
29. 
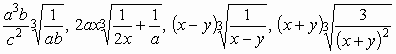
30. 
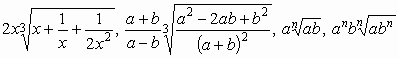
A gyökvonás azonosságainak felhasználásával végezzük el a következő műveleteket!
Példák:
a) 
,
b)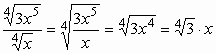 
,
c)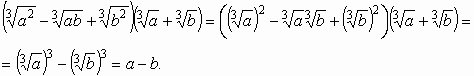 
31. 
32. 
33. 
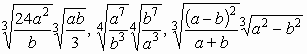
34. 
35. 
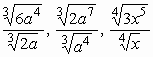
36. 
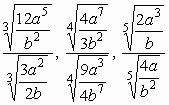
37. 
38. 
39. 
Az alábbi kifejezéseket írjuk fel egyetlen gyökjel segítségével!
Példa: 
40. 
41. 
42. 
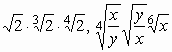
Tört számlálójának vagy nevezőjének gyöktelenítése
Négyzetgyökös kifejezéseket tartalmazó tört számlálójának vagy
nevezőjének gyöktelenítéséről már volt szó. Ritkábban, de előfordulhat, hogy n-edik gyököt tartalmazó törtre kell elvégeznünk a gyöktelenítést. Ha a gyöktelenítendő kifejezés egytagú, akkor egy egyszerű bővítéssel elérhetjük célunkat. Példaként gyöktelenítsük az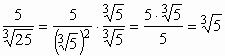
tört nevezőjét: 
.
Két- vagy többtagú kifejezés gyöktelenítése nagyon bonyolult is lehet. Ilyenkor általában − de nem mindig− az alábbi azonosságok alkalmazhatók (esetleg többször is):
(n pozitív egész) vagy
(n páratlan).
Példaként gyöktelenítsük az 
.
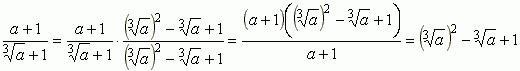Feladatok
Gyöktelenítsük a nevezőket!
43. 
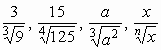
44. 
Hatványfüggvények, gyökfüggvények
Az R®
R, 
(n 1-nél nagyobb egész szám) alakú függvényeket hatványfüggvényeknek nevezzük. A négyzetre emelés függvénye is hatványfüggvény. Grafikonja parabola alakú. A többi hatványfüggvény grafikonja nem parabola, még akkor sem, ha
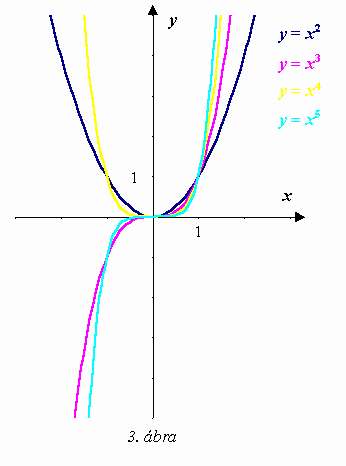
A páratlan hatványkitevőjű hatványfüggvények inverzei a páratlan gyökkitevőjű gyökfüggvények. Általános
alakjuk: R ® R,
, ahol k pozitív egész szám.
A páros gyökkitevőjű gyökfüggvények a páros hatványkitevőjű hatványfüggvényeknek a nem negatív számok halmazára való leszűkítéseinek az inverzei. Általános alakjuk:
R\R− ® R,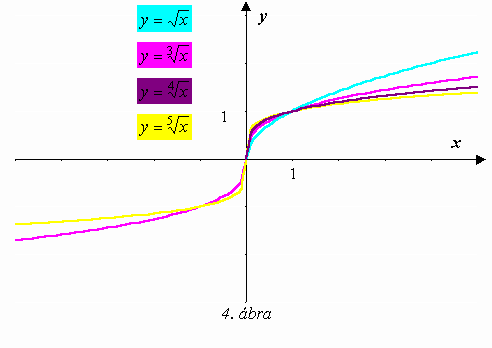
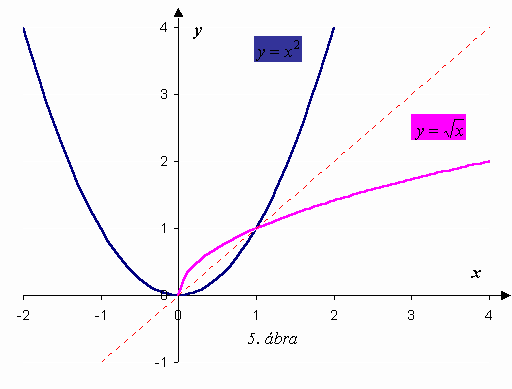
, ahol k pozitív egész szám. A 4. ábrán közös koordinátarendszerben ábrázoltunk néhány gyökfüggvényt.
Egy függvény és inverze grafikonja tengelyesen szimmetrikus az y=x egyenletű egyenesre. Ezt a kapcsolatot láthatjuk az 5. és 6. ábrákon.
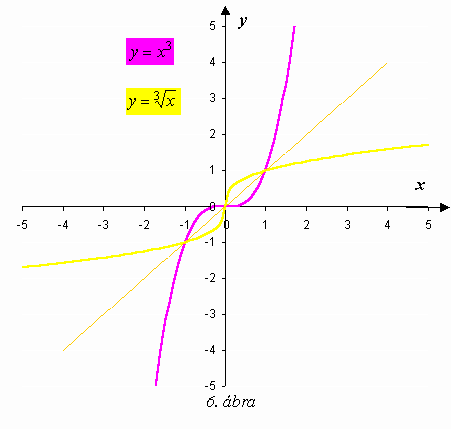
Megjegyzés
Már az időszámításunk előtt néhány évezreddel is születtek olyan táblázatok, amelyeket mennyiségek egymáshoz rendelésének tekinthetünk.
Descartes a függvényt mennyiségek megfeleltetéseként értelmezte. A Newton és Leibniz által felfedezett differenciálszámítás (a végtelenül kicsi, ún. infinitezimális mennyiségekkel való számolás) megkövetelte a függvényfogalom tisztázását. Néhány matematikus, aki kulcsfontosságú szerepet játszott a mai függvényfogalom kialakításában: Cauchy, Dirichlet, Cantor, Jordan, Weierstrass, Riemann.
Maga a függvény
elnevezés Leibniztől származik.