Ebben a fejezetben néhány jól használható tételt bizonyítunk be a
hasonlóság segítségével. Először a háromszögekkel foglalkozunk, majd a kör érintői és szelői közötti összefüggések következnek.Minden háromszögre teljesül az úgynevezett
szögfelező tétel:A háromszög belső szögfelezője a szemközti oldalt a szomszédos oldalak arányában osztja.
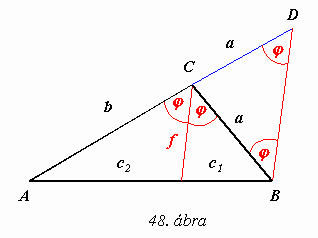
Bizonyítás (48. ábra)

Az ABC háromszög C
-ből induló szögfelezője (f) a szemközti oldalt c1 és c2 hosszúságú részekre osztja. Húzzunk párhuzamost a háromszög B csúcsán át f-fel, ez az AC oldal meghosszabítását D-ben messe. A párhuzamosság miatt a j -vel jelölt szögek egyenlők. Így a BCD háromszög egyenlő szárú, azaz CD = a. Alkalmazzuk a párhuzamos szelők tételét a következő szereposztásban: AD és BD az adott egyenesek, f és BD a párhuzamos szelők. Máris írhatjuk, hogy
A derékszögű háromszögre vonatkozó egyszerű összefüggéseket vizsgálunk (
49. ábra).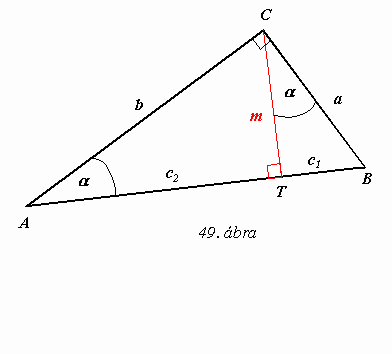
Az ABC
derékszögű háromszög átfogójához tartozó magassága (m) az átfogót c1, c2 hosszúságú darabokra osztja. Ezeket a darabokat −szokásos szóhasználattal élve− az átfogó szeleteinek nevezzük. Az ábrán a -val jelölt szögek merőleges szárú hegyesszögek, ezért egyenlők. Az ABC, ACT és CBT háromszögek páronként hasonlók, mert két-két megfelelő szögük egyenlő (a és a derékszög), így megfelelő oldalaik aránya is egyenlő. A két kisebb háromszög hasonlóságából: ![]() A kapott összefüggés a magasságtétel, szokásos megfogalmazásban:
A kapott összefüggés a magasságtétel, szokásos megfogalmazásban:
Most hasonlítsuk össze az eredeti háromszöget a BCT háromszöggel: ![]() Az eredeti és az ACT háromszögek hasonlóságából a
Az eredeti és az ACT háromszögek hasonlóságából a ![]() összefüggés adódik. Az utóbbi eredményeket szavakkal megfogalmazva: a derékszögű háromszög befogója mértani közepe az átfogónak és a befogó átfogóra eső merőleges vetületének. Ez az állítás a befogótétel.
összefüggés adódik. Az utóbbi eredményeket szavakkal megfogalmazva: a derékszögű háromszög befogója mértani közepe az átfogónak és a befogó átfogóra eső merőleges vetületének. Ez az állítás a befogótétel.
Körhöz húzott érintő- és szelőszakaszok
A körhöz
húzott érintő- és szelőszakaszokkal kapcsolatban két állítást fogalmazunk meg.A körhöz húzott érintő- és szelőszakaszok tétele:
Külső pontból a körhöz húzott érintőszakasz mértani közepe a ponton áthaladó szelő szeleteinek
(50. ábra).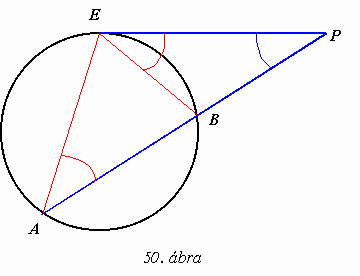
A P
külső pontból a körhöz húzott érintőszakasz PE, a szelőszakaszok PA és PB. Az ábrán piros színű körívvel jelölt szakaszok a kisebbik EB ívhez tartozó kerületi szögek, ezért a kerületi szögek tétele alapján egyenlők. Az AEP és az EBP háromszögek hasonlók, mert megegyezik két megfelelő szögük, tehát megfelelő oldalaik aránya egyenlő:Az előző tétel közvetlen következménye a külső pontból körhöz húzott szelőszakaszok tétele:
A külső pontból körhöz húzott szelők szeleteinek szorzata állandó.
A fent említett tételeken kívül még nagyon sok érdekes összefüggés bizonyítható a hasonlóság segítségével. A teljesség igénye nélkül felsorolunk néhányat.
A síkon azon pontok halmaza, amelyeknek egy szakasz két végpontjától való távolságaránya egy 1-től különböző állandó, kör (
Apollóniosz-kör).A háromszög magasságpontja, súlypontja és a háromszög köré írható kör középpontja egy egyenesre illeszkedik. A súlypont a másik két pont magasságponttól távolabbi harmadoló pontja. (
Euler-egyenes).A háromszög oldalainak felezőpontjai, magasságainak talppontjai és a magasságpontot a csúcsokkal összekötő szakaszok felezőpontjai egy körön vannak (
Feuerbach-kör).A húrnégyszög átlóinak szorzata egyenlő a szemközt
i oldalak szorzatai öszzegével (Ptolemaiosz tétele).Feladatok
181. Egy háromszög oldalainak hossza 7 cm, 6 cm , 5,5 cm. Az 5,5 cm-es oldalhoz tartozó szögfelező mekkora részekre osztja az oldalt?
182. Egy egyenlő szárú
háromszög alapja 6 cm, szárai 8 cm hosszúak. Mekkora részekre bontja a szárakat a hozzájuk tartozó magasság?183. Egy derékszögű háromszög befogóinak aránya 5:6, az átfogó 122 cm hosszú. Határozzuk meg az átfogó szeleteit!
184. Egy derékszögű háromszög be
fogóinak aránya 3:2. Az átfogó egyik szelete 2 cm-rel nagyobb a másiknál. Mekkora az átfogó?185. Egy derékszögű háromszög befogóinak aránya 3:7, az átfogóhoz tartozó magasság 42 cm. Határozzuk meg az átfogó szeleteit!
186. Egy derékszögű háromszög átfogój
ának szeletei 4 cm és 12 cm. Mekkorák a befogók és az átfogóhoz tartozó magasság?187. Egy derékszögű háromszög egyik befogója 5 cm, ennek vetülete az átfogón 2 cm. Mekkora az átfogó és a másik befogó?
188. Adott két távolság összege. Szerkesszük meg a mértani közepüket!
189. Egy kör belsejében levő ponton át húzzunk két tetszés szerinti szelőt. Bizonyítsuk be, hogy a szelők szeleteinek szorzata egyenlő!